Formula
The operation is indicated by an asterisk. The convolution of two functions is equal to the product of the two functions integrated. Since images are composed of pixels, functions are discrete when processing images.
Convolution of two functions:
$ f(x) * g(x) = \displaystyle\int_{-\infty}^{\infty} f(\tau) ⋅ g(x - \tau) \, d\tau $
Visualisation
The process of convolution can be thought of as one function shifting through the other, and at each point the result is the integral of the product of overlapping values, or the sum in the case of discrete convolution.
Guaussian blur
A Gaussian kernel can be used to smooth a function. This can be good for noise, but information may be lost in the process. A rectangular kernel also smoothes, but might give an abnormal, chunky result for images.
2D Convolution
The formula can be extended to two dimensions to convolve images. The kernel slides through the image changing the values of each pixel based on its neigbourhood of a given size.
$ f(x, y) * g(x, y) = \displaystyle\iint_{-\infty}^{\infty} f(\tau, \mu) ⋅ g(x - \tau, y - \mu) \, d\tau d\mu $

*
=

Properties
Convolution is commutative and associative, so for example an operation using a symmetric Gaussian 2D kernel can be split into 2 consecutive one-dimensional convolutions, reducing the number of operations.
$ f * g = g * f $
$ (f * g) * h = f * (g * h) $
Feature extraction
Convolutional Neural Networks (CNNs) form their own kernels to extract features from images when they are training on a given dataset. The neural network usually trains on the output of multiple convolutional layers.

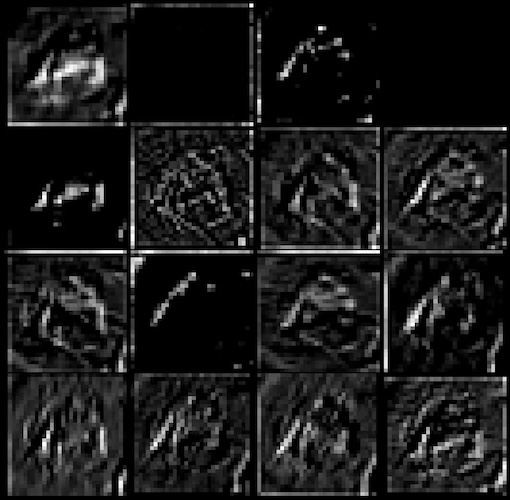

# Rodrigo Silva: Exploring Feature Extraction with CNNs, Towards Data Science
#
https://towardsdatascience.com/exploring-feature-extraction-with-cnns-345125cefc9a
Fourier transform
Just like a function, a photo can be converted into frequency domain. The convolution operation becomes a simple multiplication in frequency domain, so by applying the FFT algorithm to both the image and kernel and then multiplying them together, convolution is achieved. After converting back (IFFT), the result is the same as in the spatial domain by sliding the filter through. The really useful feature of this method, besides its speed, is that it can be done backwards. Deconvolution is simply a division in frequency domain, and by estimating kernels reconstruction of poor quality or blurred photographs can be performed.
$ f(x, y) * g(x, y) = F(u, v) ⋅ G(u, v) $


Help
Install SciPy: https://pypi.org/project/scipy
Convolution Excel table: Download
Boglárka (LQ) image: Download
Inster image: Download
Source code: 2D Convolution
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from scipy.signal import convolve2d
# Open the image using PIL
image = Image.open("path-to-resources/boglarka_low.jpg")
# Convert image to a NumPy array
data = np.array(image, dtype=np.uint8)
# Define a 5x5 kernel
kernel = np.array([[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1]])
# Normalize the kernel
kernel = kernel / kernel.sum()
# Perform the 2D convolution on each color channel
convolved_image_channels = [convolve2d(data[:, :, i], kernel) for i in range(3)]
# Combine the three channels back into one array
convolved_image = np.stack(convolved_image_channels, axis=-1).astype(np.uint8)
# Display images
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(image)
ax[0].set_title("Original Image")
ax[0].axis("off")
ax[1].imshow(convolved_image)
ax[1].set_title("Convolved Image")
ax[1].axis("off")
plt.show()
Source code: Deconvolution
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft2, ifft2
# Open the image using PIL
# Villanyautó teszt: Hyundai Inster – kisautózni jó! - Villanyautósok
# https://villanyautosok.hu/2025/02/26/villanyauto-teszt-hyundai-inster-kisautozni-jo
image = Image.open("path-to-resources/inster.jpeg").convert("L")
# Convert image to a NumPy array
data = np.array(image, dtype=np.uint8)
# Function to build a motion blur kernel
def build_blur_kernel(size, angle, img_shape):
# Create empty matrix and calculate its center
kernel = np.zeros((size, size))
center = size // 2
# Calculate elements of the kernel matrix
for i in range(size):
x = int(center + (i - center) * np.cos(np.deg2rad(angle)))
y = int(center + (i - center) * np.sin(np.deg2rad(angle)))
if 0 <= x < size and 0 <= y < size:
kernel[y, x] = 1
# Normalize the kernel
normalized_kernel = kernel / kernel.sum()
return normalized_kernel
# Function to apply convolution in frequency domain
def apply_blur_fft(image, kernel):
# Convert the image and the kernel to frequency domain
fft_image = fft2(image)
fft_kernel = fft2(kernel, s = image.shape)
# Perform convolution in frequency domain (multiplication)
blurred_image = fft_image * fft_kernel
# Convert blurred image back to spatial domain
blurred_image = np.abs(ifft2(blurred_image))
blurred_image = np.clip(blurred_image, 0, 255).astype(np.uint8)
return blurred_image
# Function to apply deconvolution
def apply_deconvolution(image, kernel, K=0.01):
# Convert the image and the kernel to frequency domain
fft_image = fft2(image)
fft_kernel = fft2(kernel, s=image.shape)
# Replace 0 values with a small value before division
fft_kernel = np.where(fft_kernel == 0, 1e-8, fft_kernel)
# Perform deconvolution in frequency domain (division)
restored_image = fft_image / fft_kernel * (np.abs(fft_kernel) ** 2 / (np.abs(fft_kernel) ** 2 + K))
# Convert restored image back to spatial domain
restored_image = np.abs(ifft2(restored_image))
restored_image = np.clip(restored_image, 0, 255).astype(np.uint8)
return restored_image
# Create motion blur kernel
kernel = build_blur_kernel(size = 10, angle = 30, img_shape = data.shape)
# Apply motion blur using FFT
blurred_image = apply_blur_fft(image = data, kernel = kernel)
# Apply deconvolution
restored = apply_deconvolution(image = blurred_image, kernel = kernel)
# Display images
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
ax[0].imshow(data, cmap="gray")
ax[0].set_title("Original Image")
ax[0].axis("off")
ax[1].imshow(blurred_image, cmap="gray")
ax[1].set_title("Blurred Image")
ax[1].axis("off")
ax[2].imshow(restored, cmap="gray")
ax[2].set_title("Restored Image")
ax[2].axis("off")
plt.show()