Konvolúció

Képlete

A műveletet csillag jelöli. Két függvény konvolúciója egyenlő a függvények szorzatával a teljes értelmezési tartományon integrálva. Mivel a képek pixelekből állnak, képfeldolgozáskor a függvények diszkrétek.

Két függvény konvolúciója:

$ f(x) * g(x) = \displaystyle\int_{-\infty}^{\infty} f(\tau) ⋅ g(x - \tau) \, d\tau $

Vizualizációja

A konvolúció folyamata elképzelhető úgy, hogy az egyik függvény eltolva végighalad a másikon, és minden ponton az eredmény az átfedő értékek szorzatának integrálja, diszkrét konvolúció esetén az összege.

Guaussian blur

Egy Gauss-görbe alakú kernellel elsimítható egy függvény. Ez jó hatással lehet a zajra, azonban az információ is elveszhet közben. A négyszög alakú kernel is simít, de képek esetén rendellenes, darabos eredményt adhat.

2D Konvolúció

A képlet bővíthető, két változóval értelmezhetővé válik képek konvolúciója. A kernel végigcsúszik a képen, és közben az adott pixelnek és az adott méretű környezetének az értékeit, így a kép megjelenését változtatja.

$ f(x, y) * g(x, y) = \displaystyle\iint_{-\infty}^{\infty} f(\tau, \mu) ⋅ g(x - \tau, y - \mu) \, d\tau d\mu $

Tulajdonságok

A konvolúció kommutatív és asszociatív, így például a Gaussian-blur szimmetrikus 2D kernelt használó művelet szeparálható 2 egymás utáni egydimenziós konvolúcióra, ezzel csökkentve a műveletek számát.

$ f * g = g * f $

$ (f * g) * h = f * (g * h) $

Feature extraction

A Konvolúciós Neurális Hálók (CNN) saját maguknak alkotnak különböző kerneleket, amelyekkel az adott adathalmaz tanulásakor jellemzőket nyernek ki a képekből. A tanulás a konvolúciók eredményein történik.

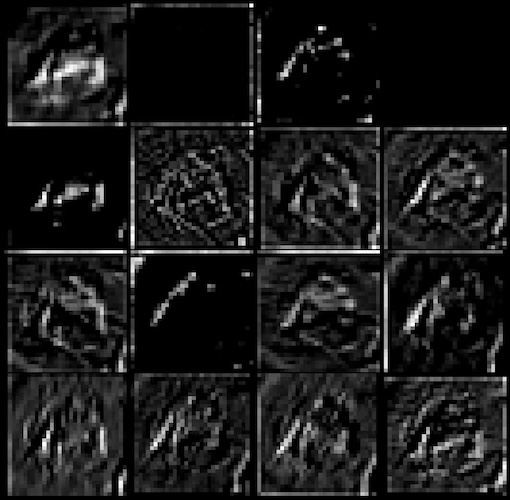
# Rodrigo Silva: Exploring Feature Extraction with CNNs, Towards Data Science
# https://towardsdatascience.com/exploring-feature-extraction-with-cnns-345125cefc9a

Fourier-transzformáció

Ahogyan egy függvény, úgy egy fénykép is kezelhető frekvenciatartományban. A konvolúció művelet ekkor egy egyszerű szorzássá alakul, így az FFT algoritmust alkalmazva a képre és kernelre, majd összeszorozva azokat megvalósul a konvolúció. Visszaalakítás (IFFT) után az eredmény ugyan az, mint térbeli tartományban a szűrő végigcsúsztatásával. Az igazán hasznos tulajdonsága a módszernek a sebessége mellett az, hogy visszafelé is elvégezhető. A dekonvolúció frekvenciatartományban osztás, kernelek becslésével rekonstruálhatók rossz minőségű vagy elmosódott fényképek.

$ f(x, y) * g(x, y) = F(u, v) ⋅ G(u, v) $

Segédlet

SciPy telepítése: https://pypi.org/project/scipy

Konvolúció Excel-tábla: Letöltés

Boglárka (LQ) fénykép: Letöltés

Inster fénykép: Letöltés

Forráskód: 2D KonvolúcióMásolás

        
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

# Open the image using PIL
image = Image.open("path-to-resources/boglarka_low.jpg")

# Convert image to a NumPy array
data = np.array(image, dtype=np.uint8)

# Define a 5x5 kernel 
kernel = np.array([[1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1],
                   [1, 1, 1, 1, 1, 1, 1]])

# Normalize the kernel
kernel = kernel / kernel.sum()

# Perform the 2D convolution on each color channel
convolved_image_channels = [convolve2d(data[:, :, i], kernel) for i in range(3)]
# Combine the three channels back into one array
convolved_image = np.stack(convolved_image_channels, axis=-1).astype(np.uint8)

# Display images
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(image)
ax[0].set_title("Original Image")
ax[0].axis("off")
ax[1].imshow(convolved_image)
ax[1].set_title("Convolved Image")
ax[1].axis("off")
plt.show()
          
        

Forráskód: DekonvolúcióMásolás

        
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft2, ifft2

# Open the image using PIL
# Villanyautó teszt: Hyundai Inster – kisautózni jó! - Villanyautósok
# https://villanyautosok.hu/2025/02/26/villanyauto-teszt-hyundai-inster-kisautozni-jo
image = Image.open("path-to-resources/inster.jpeg").convert("L")

# Convert image to a NumPy array
data = np.array(image, dtype=np.uint8)

# Function to build a motion blur kernel
def build_blur_kernel(size, angle, img_shape):
    # Create empty matrix and calculate its center
    kernel = np.zeros((size, size))
    center = size // 2
    # Calculate elements of the kernel matrix
    for i in range(size):
        x = int(center + (i - center) * np.cos(np.deg2rad(angle)))
        y = int(center + (i - center) * np.sin(np.deg2rad(angle)))
        if 0 <= x < size and 0 <= y < size:
            kernel[y, x] = 1
    # Normalize the kernel
    normalized_kernel = kernel / kernel.sum()
    return normalized_kernel

# Function to apply convolution in frequency domain
def apply_blur_fft(image, kernel):
    # Convert the image and the kernel to frequency domain
    fft_image = fft2(image)
    fft_kernel = fft2(kernel, s = image.shape)
    # Perform convolution in frequency domain (multiplication)
    blurred_image = fft_image * fft_kernel
    # Convert blurred image back to spatial domain
    blurred_image = np.abs(ifft2(blurred_image))
    blurred_image = np.clip(blurred_image, 0, 255).astype(np.uint8)
    return blurred_image

# Function to apply deconvolution
def apply_deconvolution(image, kernel, K=0.01):
    # Convert the image and the kernel to frequency domain
    fft_image = fft2(image)
    fft_kernel = fft2(kernel, s=image.shape)
    # Replace 0 values with a small value before division
    fft_kernel = np.where(fft_kernel == 0, 1e-8, fft_kernel)
    # Perform deconvolution in frequency domain (division)
    restored_image = fft_image / fft_kernel * (np.abs(fft_kernel) ** 2 / (np.abs(fft_kernel) ** 2 + K))
    # Convert restored image back to spatial domain
    restored_image = np.abs(ifft2(restored_image))
    restored_image = np.clip(restored_image, 0, 255).astype(np.uint8)
    return restored_image

# Create motion blur kernel
kernel = build_blur_kernel(size = 10, angle = 30, img_shape = data.shape)
# Apply motion blur using FFT
blurred_image = apply_blur_fft(image = data, kernel = kernel)
# Apply deconvolution
restored = apply_deconvolution(image = blurred_image, kernel = kernel)

# Display images
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
ax[0].imshow(data, cmap="gray")
ax[0].set_title("Original Image")
ax[0].axis("off")
ax[1].imshow(blurred_image, cmap="gray")
ax[1].set_title("Blurred Image")
ax[1].axis("off")
ax[2].imshow(restored, cmap="gray")
ax[2].set_title("Restored Image")
ax[2].axis("off")
plt.show()