Using lenses

Focal length

The big advantage of lenses is that they can let in much more light. Interestingly, the lens was named after its plant-like shape in the early 1300s. The focal length of a lens, as opposed to the Camera Obscura, describes the ability of the lens to refract light rays. For thin lenses it can be calculated from the thin lens equation.

Thin lens equation:

$ \dfrac{1}{f} = \dfrac{1}{z_0} + \dfrac{1}{z_i} $

Camera lenses

Optical devices containing a number of lens elements, which can be characterised by a single focal length despite the fact that the light in them follows a very complex path are also called lenses. On all cameras there is a lens in front of the sensor, often interchangeable, but on smart devices, for example, it is built-in. It can be misleading that the English word "lens" means multiple things. For a lens to be attached to a camera, it must have the same mount. Many brands have their own mounts, brand independent ones are C/CS, M12.

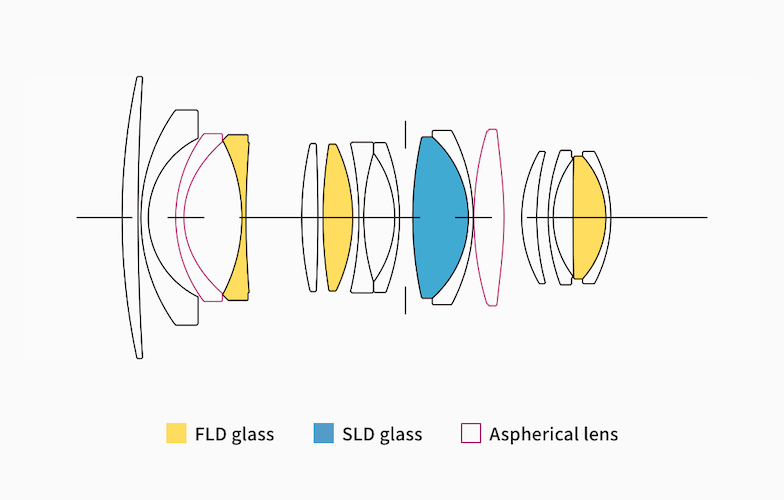
# https://www.sigma-global.com/en/lenses/c017_16_14

So-called aspherical lens elements are often found in a lens, which means that the radius of the lens arc changes from the centre to the edge. It gives a sharper image, less distortion and lets in more light.

Fresnel lens

It is a special optical lens developed by French physicist Augustin-Jean Fresnel for lighthouses. The special feature of the lens is that it is made up of several thin rings, each of which forms a small part of the refractive surface. The thickness and mass of the lens is significantly reduced, while maintaining its refractive power. It is difficult to make a good quality Fresnel lens, yet it is used in many applications, such as virtual reality (VR) glasses, projectors, car headlights and other applications where size is more important than quality.

# https://whatvr.co/reviews/htc-vive-pro-review

Aperture

By reducing the diameter of a lens, the amount of light entering it can be controlled. A lamellar system inside the lens is usually used by manufacturers to solve this variability. The aperture word officially refers to the area through which light can pass. The focal length divided by the diameter is the f-number of a lens.

f-number:

$ N = \dfrac{f}{d_{Ap.}} $

Depth of field

Because lenses refract light rays to a certain extent, only points on a specific plane in front of the lens are sharply visible on the surface of the sensor behind the lens. The plane is called the focal plane, and points outside it appear as a blurred circle on the sensor. The further away a point is, the larger the circle will be, but as the aperture is reduced, the diameter of the circles is reduced.

As long as the diameter of the blurred circle on the sensor is less than one pixel, it appears to be sufficiently sharp, meaning the points in focus are not on a single plane but on a range of planes. This is called the depth of field, which obviously depends on aperture, focal length and image distance.

Hyperfocal distance

There is a need for a lens to be able to focus to infinity. Because of the depth of field, there must be a shortest image distance somewhere beyond which all points will appear sharp, so the diameter of the blurred circle will be less than a pixel. This is the hyperfocal distance.