Gyújtótávolság
A lencsék nagy előnye, hogy sokkal több fényt képesek beengedni. Érdekesség, hogy nevét a lencse növényhez hasonlító alakjáról kapta az 1300-as évek elején. Egy lencse gyújtótávolsága a Camera Obscura-tól eltérően azt jellemzi, hogy a lencse mennyire képes megtörni a fénysugarakat. A leképezési törvénnyel számolható.
Leképezési törvény:
$ \dfrac{1}{f} = \dfrac{1}{z_0} + \dfrac{1}{z_i} $
Objektívek
Számos lencsetagot tartalmazó optikai eszközök, amelyek jellemezhetők egyetlen gyújtótávolsággal annak ellenére, hogy bennük a fény nagyon összetett utat jár be. Minden kamerán van egy objektív a szenzor előtt, sokszor ez cserélhető, de okoseszközökön például beépített. Félrevezető lehet, hogy az angol „lens” szó a lencse mellett magát az objektívet is jelenti. Ahhoz, hogy egy lencse csatlakozhasson egy kamerához, azonos bajonettel kell rendelkezniük. Sok márkának saját bajonettje van, márkafüggetlen bajonettek a C/CS, M12.

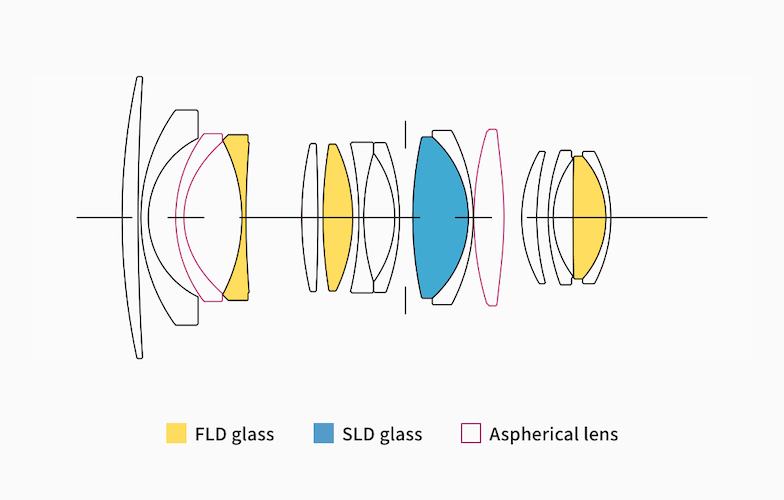
# https://www.sigma-global.com/en/lenses/c017_16_14
Gyakran találhatók úgynevezett aszférikus lencsetagok egy objektívben, amely azt jelenti, hogy a közepétől a széle felé haladva a lencse ívének sugara változik. Élesebb képet ad, kevésbé torzít és több fényt enged be.
Fresnel-lencse
A Fresnel-lencse egy olyan speciális optikai lencse, amelyet Augustin-Jean Fresnel francia fizikus fejlesztett ki világítótornyok számára. A lencse különlegessége, hogy több vékony gyűrűből áll, amelyek mindegyike egy kis részletét alkotja az összesített törőfelületnek. Jelentősen csökken a lencse vastagsága és tömege, közben megmarad a fénytörő képesség. Nehéz jó minőségű Fresnel lencsét készíteni, de mégis számos területen alkalmazzák, például virtuális valóság (VR) szemüvegekben, projektorokban, autós fényszórókban.

# https://whatvr.co/reviews/htc-vive-pro-review
Apertúra
A lencse átmérőjének csökkentésével redukálható a beérkező fény mennyisége. Az objektív belsejébe szerelt lamellás rendszerrel szokták a gyártók megoldani a variálhatóságát. Az apertúra egészen pontosan a terület, ahol a fény keresztül tud haladni. A gyújtótávolságból és a terület átmérőjéből kifejezve ez a rekeszérték.
Rekeszérték:
$ N = \dfrac{f}{d_{Ap.}} $
Mélységélesség
Mivel a lencsék egy adott mértékben törik meg a fénysugarakat, a lencse mögötti szenzor felületén csak azok a pontok jelennek meg élesen, amelyek egy konkrét síkon találhatók a lencse előtt. A sík neve fókuszsík, és a rajta kívül eső pontok homályos körként jelennek meg a szenzoron. Minél távolabbi egy pont, annál nagyobb kör lesz, de az apertúra csökkentésével a köröknek az átmérője is csökken.
Ameddig a szenzoron megjelnő elmosódott kör átmérője kisebb, mint egy pixel, addig az megfelelően élesnek látszik, vagyis a fókuszban lévő pontok nem egy síkban értelmezhetők, hanem egy tartományban. Ezt nevezik mélységélességnek, amely nyilvánvalóan függ a rekeszértéktől, gyújtótávolságtól és a képtávolságtól is.


Hiperfokális távolság
Nyilvánvalóan szükség van arra, hogy egy objektív a végtelenbe is tudjon fókuszálni. A mélységélesség miatt valahol kell lennie egy olyan legrövidebb képtávolságnak, amelyen túl minden pont élesen jelenik meg, tehát az elmosódott kör átmérője kisebb lesz, mint egy pixel. Ez a képtávolság a hiperfokális távolság.
$ H = \dfrac{f^2}{N ⋅ c} + f $
$ H \approx \dfrac{f^2}{N ⋅ c} $